【Unity】【C#】CSharp算法学习笔记

发表于 更新于

交换两个数的值

元组解构

该方法也会创建一个临时变量（元组）

1
(a, b) = (b, a)

异或

a,b 不能是同一地址。由于异或的特性，如果两个是同一地址会导致输出为0

1
2
3
a = a ^ b;
b = a ^ b;
a = a ^ b;

拓展：异或

相同则为0，不同则为1，可以理解成“不进位的加法”

  • 0 ^ N = N N ^ N = 0
  • 满足交换律和结合律

加减

同样a,b不能是同一地址，不然在第二步的时候，自己减自己等于0

1
2
3
a = a + b;
b = a - b;
a = a - b;

时间复杂度

常数操作的次数

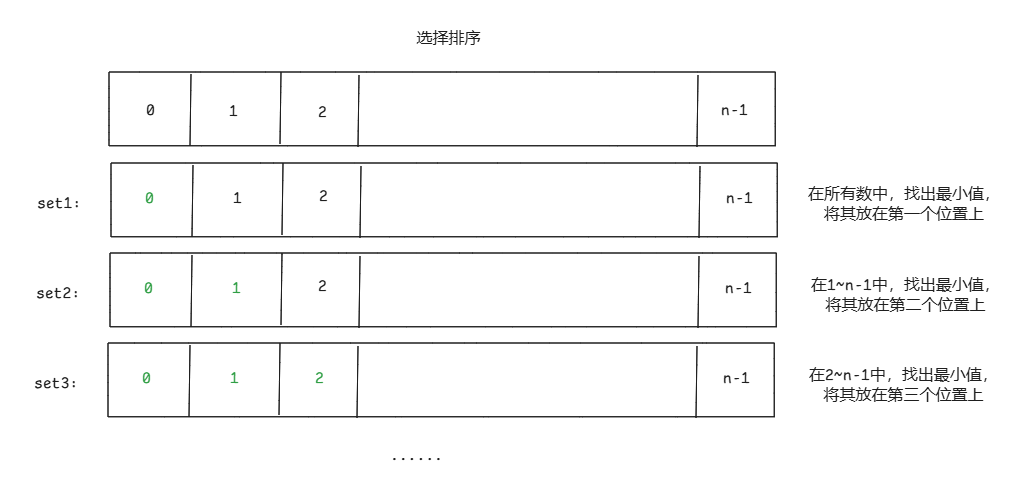
排序算法

选择排序

简单选出最小的数，将其放置在最前面

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
static void SelectionSort(int[] arr)
{
    if (arr == null || arr.Length < 2) return;	// 直接返回不需要排序的数组
    for (int i = 0; i < arr.Length; i++)
    {
        int minIndex = i;
        for (int j = i + 1; j < arr.Length; j++)		// 寻找最小值的序号
        {
            if (arr[j] < arr[minIndex])
                minIndex = j;
        }
        Swap(arr, i, minIndex);							// 找出最小值的序号后与最前面的数值交换位置
    }
}

static void Swap(int[] arr, int a, int b)
{
    int temp = arr[a];
    arr[a] = arr[b];
    arr[b] = temp;
}


int[] nums = new[] { 5, 2, 7, 3, 9, 1, 8, 6 };
nums = QuickSort(nums);
Console.WriteLine(string.Join(", ", nums));

时间复杂度计算：

set1：

  • n-1次获取数值
  • n-1次比较
  • 1次交换

set2：

  • n-2次获取数值
  • n-2次比较
  • 1次交换

……

由等差数列公式可知：

  • 获取数值共：n(n+1)/2次
  • 比较共：n(n+1)/2次
  • 交换共：n次

三者相加最大的阶乘为2，所以时间复杂度为O(n^2)

拓展：等差数列公式

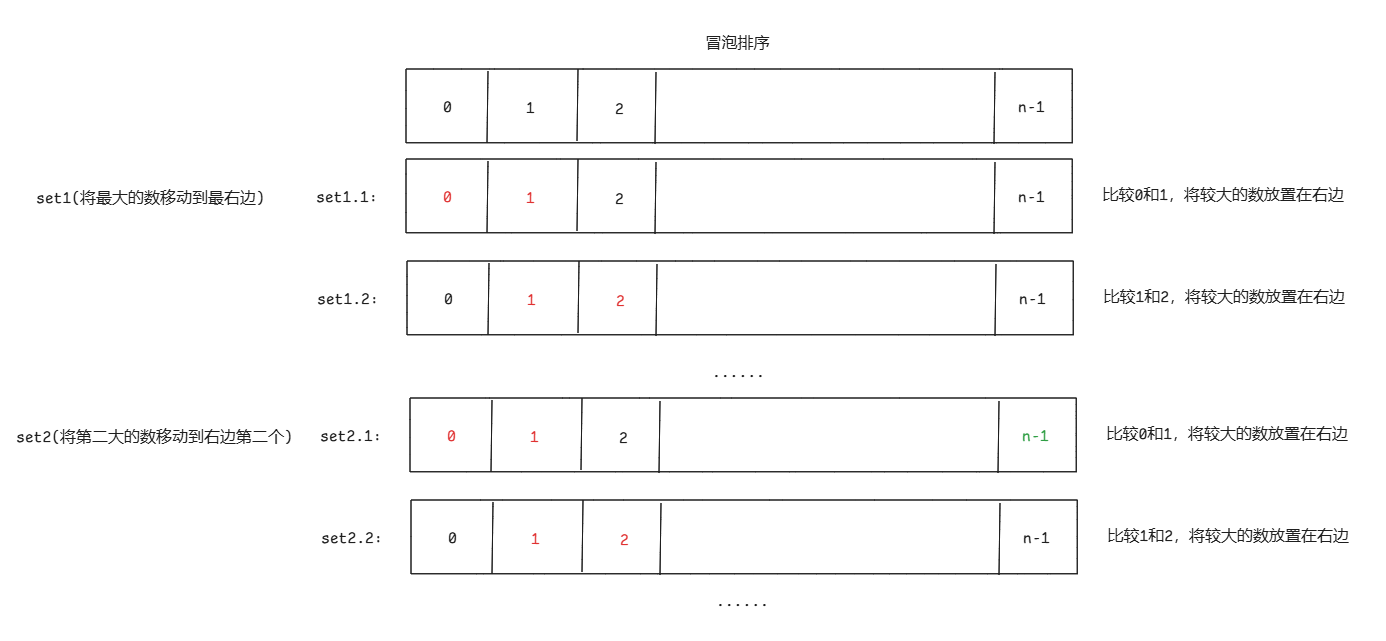
冒泡排序

相邻的两个数相比较，一步一步的将最大的数移动到最右边

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
static void BubbleSort(int[] arr)
{
    if (arr == null || arr.Length < 2) return;
    for (int k = 0; k < arr.Length; k++)	// 共需要移动length的次数
    {
        for (int i = 0; i < arr.Length - 1; i++)
        {
            if (arr[i] > arr[i + 1])		// 将最大的值移动到最右边
            {
                Swap(arr, i, i + 1);
            }
        }
    }
}
// 冒泡排序不会与自己交换位置，所以可以使用异或交换值
static void Swap(int[] arr, int a, int b)
{
    arr[a] = arr[a] ^ arr[b];
    arr[b] = arr[a] ^ arr[b];
    arr[a] = arr[a] ^ arr[b];
}

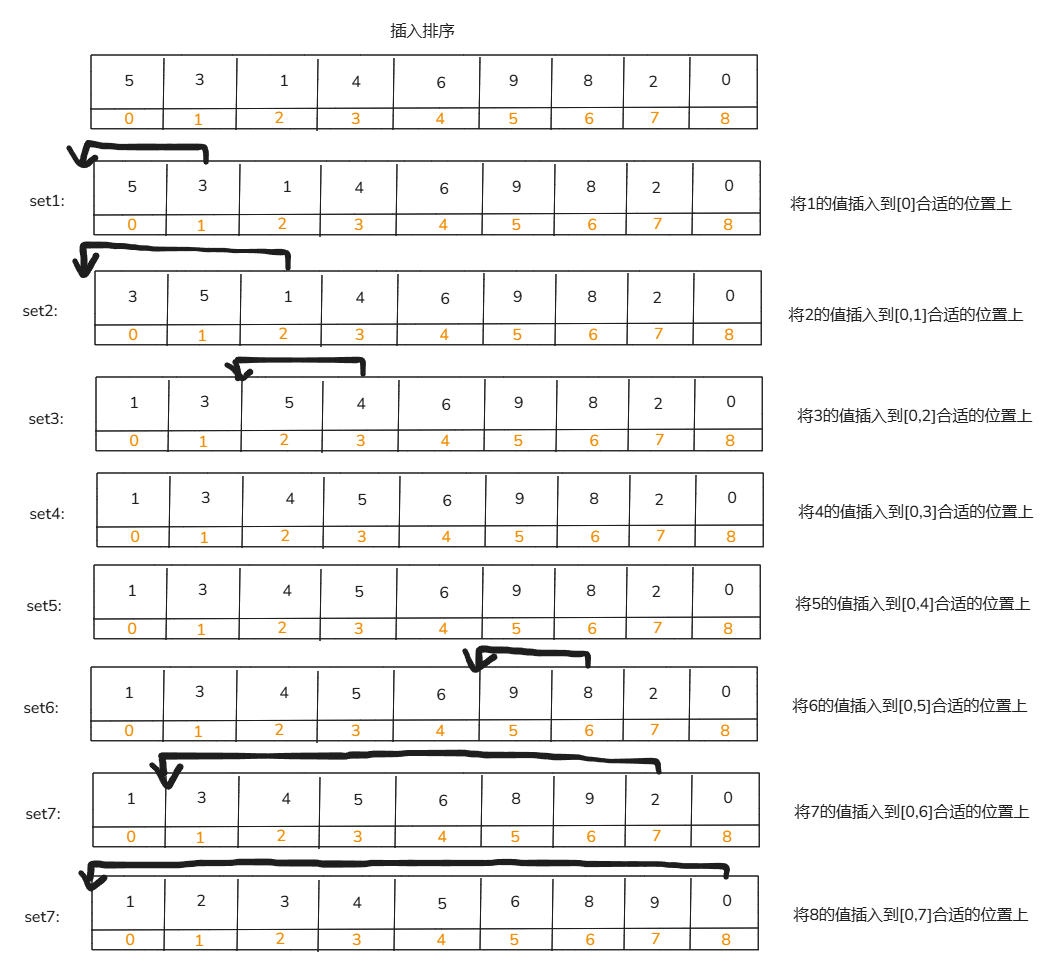
插入排序

第一步：将[0]排序；第二步：将[0,1]排序；第三步：将 [0,2]排序；第四步：将[0,3]排序……

具体插入实现方法（set7）：

当我们到达set7时，[0,6]一定是有序的。所以从右往左一个一个比较

  • 若arr[7]小于arr[6]两者交换位置。
1
2
3
4
5
6
7
8
9
10
11
static void InsertionSort(int[] arr)
{
    if (arr == null || arr.Length < 2) return;
    for (int i = 1; i < arr.Length; i++)
    {
        for (int j = i - 1; j >= 0 && arr[j] > arr[j + 1]; j--)	// 当j>=0，且arr[j]大于其右边的数，两者交换位置
        {
            Swap(arr, j, j + 1);
        }
    }
}

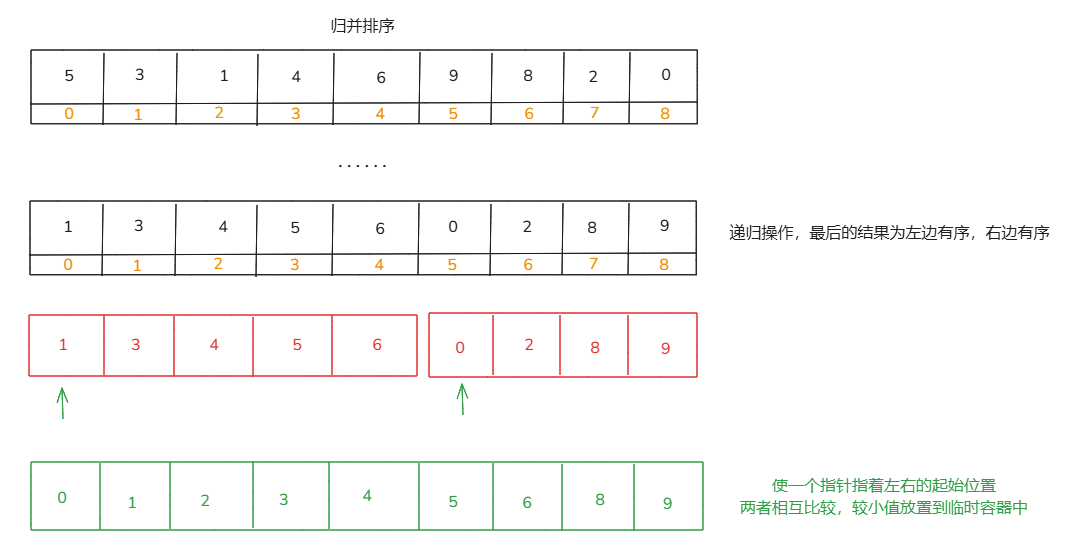
归并排序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
static void MergeSort(int[] arr, int left, int right)
{
    if (left >= right) return;
    int mid = left + ((right - left) >> 1);
    MergeSort(arr, left, mid);
    MergeSort(arr, mid + 1, right);
    merge(arr, left, mid, right);
}

static void merge(int[] arr, int L, int M, int R)
{
    int[] temp = new int[R - L + 1];
    int i = 0, p1 = L, p2 = M + 1;

    while (p1 <= M && p2 <= R)
        temp[i++] = arr[p1] <= arr[p2] ? arr[p1++] : arr[p2++];
    while (p1 <= M)
        temp[i++] = arr[p1++];
    while (p2 <= R)
        temp[i++] = arr[p2++];
    for (int j = 0; j < temp.Length; j++)
        arr[L + j] = temp[j];
}

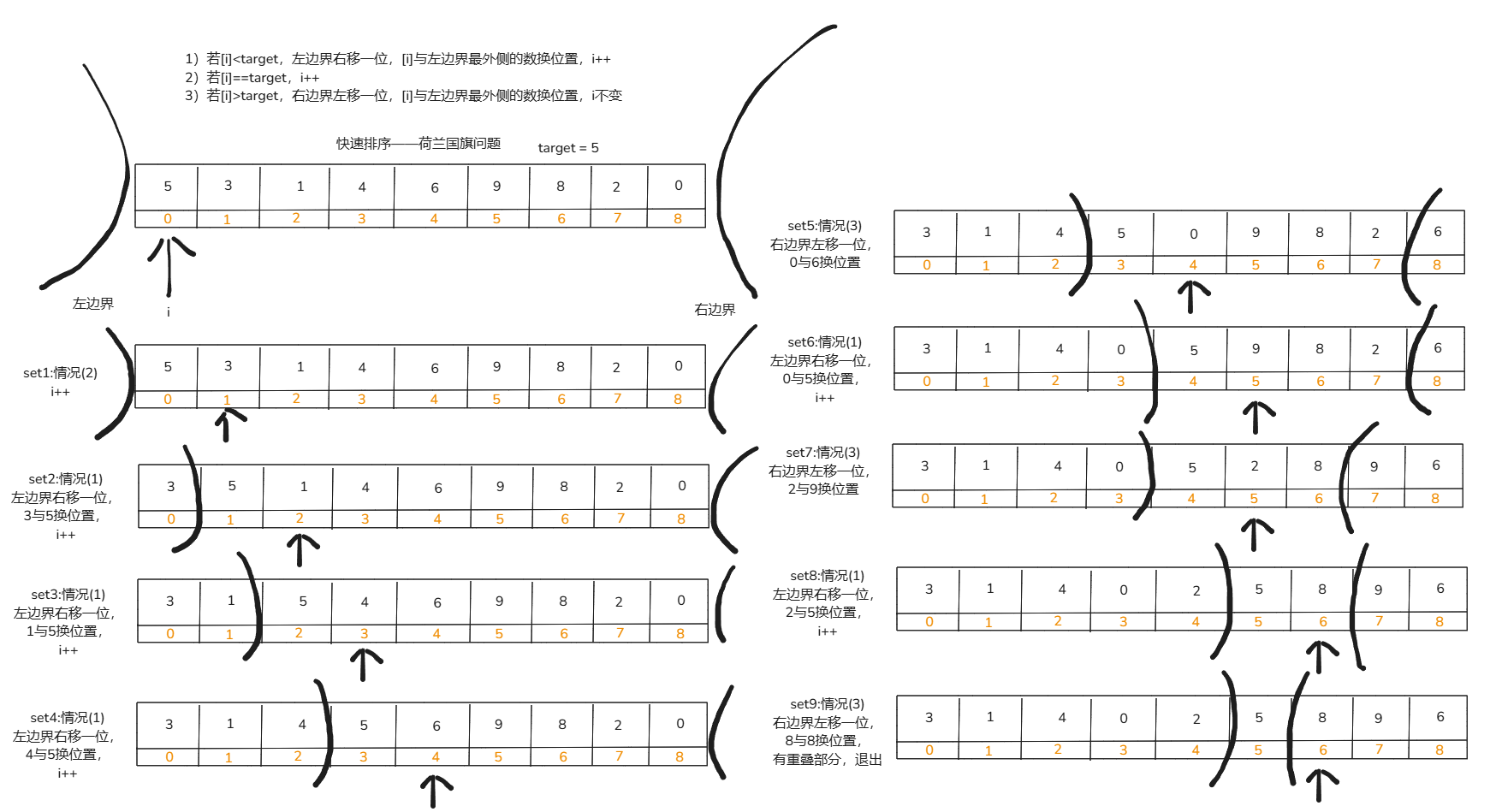
快速排序

在学习快速排序前先看一下荷兰国旗问题

现有一个数组arr和target，要求小于target的数放在数组左边，大于target的放在数组的右边，等于target的数放在中间

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
// 荷兰国旗
static void Partition(int[] arr, int target)
{
    int left = -1, right = arr.Length;
    int i = 0;
    while (i < right)
    {
        if (arr[i] < target)
            Swap(arr, ++left, i++);
        else if (arr[i] > target)
            Swap(arr, i, --right);
        else
            i++;
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
// 快速排序
static void QuickSort(int[] arr, int L, int R)
{
    if (L >= R) return;
    int random = new Random().Next(R - L + 1);	// 随机取出一个数将其作为基准，这样可以将事件复杂度降低为O(N*logN)
    Swap(arr, L + random, R);
    int[] p = Partition(arr, L, R);
    QuickSort(arr, L, p[0] - 1);  // < 区域
    QuickSort(arr, p[1] + 1, R);  // > 区域
}

/// <summary> 荷兰国旗问题 </summary>
/// <returns>返回等于区域的左右边界</returns>
static int[] Partition(int[] arr, int L, int R)
{
    int less = L - 1;  // < 区域右边界
    int more = R;      // > 区域左边界
    while (L < more)
    {
        if (arr[L] < arr[R])    // 当指针上的数小于基准数时，将指针上的数与 < 区域的下一个数交换，指针右移
            Swap(arr, ++less, L++);
        else if (arr[L] > arr[R])   // 当指针上的数大于基准数时，将指针上的数与 > 区域的前一个数交换，指针不动
            Swap(arr, --more, L);
        else                       // 当指针上的数等于基准数时，指针右移
            L++;
    }
    Swap(arr, R, more);         // 将基准数与 > 区域的第一个数交换
    return new[] { less + 1, more };    // 返回等于区域的左右边界
}

二分法

在有序数列中查找某个值

1
2
3
4
5
6
7
8
9
10
static void fun(int[] arr, int target)
{
    int m = arr.Length / 2;
    if (arr[m] == target)
        Console.WriteLine(m);
    else if (arr[m] > target)
        fun(arr[..m], target);
    else
        fun(arr[(m + 1)..], target);
}

在有序数列中查找最大值

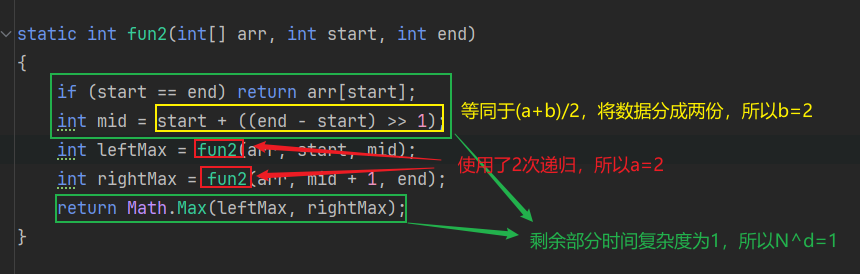
1
2
3
4
5
6
7
8
static int fun2(int[] arr, int start, int end)
{
    if (start == end) return arr[start];
    int mid = start + ((end - start) >> 1);
    int leftMax = fun2(arr, start, mid);
    int rightMax = fun2(arr, mid + 1, end);
    return Math.Max(leftMax, rightMax);
}

递归方法的时间复杂度：

master公式的使用：

使用master公式的前提条件是在递归的时候平分数据，如fun2将数平方成了2份，也可以平分成3份、2/3份，只要是平分就行。
$$
T(N) = a * T (\frac{N}{b}) + O(N^d)
$$
a：一个方法中使用多少次递归

b：递归的时候，将数据平方成了多少份

d：除去递归函数外其他部分的时间

最终的结果为：
$$
T(N) = 2 * T (\frac{N}{2}) + O(N^0)
$$
当递归函数满足master公式时，可以通过a、b、d得到算法复杂度
$$
\begin{split}
&若log_b{a}<d，则O(N^d) \
&若log_b{a}>d，则O(N^{log_b{a}}) \
&若log_b{a}=d，则O(N^d*logN)
\end{split}
$$

所以最后的时间复杂度为O(N)