【Unity】向量

发表于 更新于

现有两个点a, b

假设Y值都相等

  • a到b的向量：var direction = a - b;
  • 以a为中心，世界坐标为方向，b在a的什么弧度上：var angleRag = math.atan2(direction.z, direction.x);
  • 什么角度上：var angleDeg = math.degrees(angleRag)

向量之间的计算

点乘(内积)运算

a 与 b 的点乘（也称内积）公式如下

$$
\vec{a}\vec{b}=|\vec{a}||\vec{b}|cosθ (0°<θ<180°)
$$
若a=(ax, ay, az)，b=(bx, by, bz)，则
$$
\vec{a}\vec{b}=a_xb_x+a_yb_y+a_z*b_z
$$
在unity中，提供了Vector3.Dot()方法计算两个向量的点乘

1
2
3
4
5
6
7
8
9
10

Vector3 vectorA = new Vector3(1, 2, 3);
Vector3 vectorB = new Vector3(4, 5, 6);

float dotProduct = Vector3.Dot(vectorA, vectorB);

// 结果输出: 32，32>0，即向量a,b的夹角为锐角
// dotProduct > 0，为锐角
// dotProduct = 0, 为直角
// dotProduct < 0, 为钝角

点乘的结果是|a||b|cosθ

  • 如果只用判断两个向量夹角的关系，则只用判断dotProduct的值就好了
  • 如果需要得到cosθ，需要除以|a||b|

叉乘(外积)运算

a 与 b 的叉乘（也称外积、向量积、叉积）公式如下
$$
|\vec{c}|=|\vec{a} \times \vec{b}|=|\vec{a}|*|\vec{b}|*sinθ
$$

若a=(a_x, a_y, a_z)，b=(b_x, b_y, b_z)，i,j,k分别为x,y,z轴的单位向量，则
$$
\vec{a}×\vec{b}=(a_yb_z-a_zb_y)\vec{i}+(a_zb_x-a_xb_z)\vec{j}+(a_xb_y-a_yb_x)\vec{k}
$$
在unity中，提供了Vector3.Cross()方法计算两个向量的叉乘

1
2
3
4
5
6
Vector3 vectorA = new Vector3(1, 2, 3);
Vector3 vectorB = new Vector3(4, 5, 6);

Vector3 crossProduct = Vector3.Cross(vectorA, vectorB);

// 结果输出: (3, -6, 3)

叉乘的结果是是一个新的向量c，c垂直与a和b所在平面，且方向由右手定则确定（当右手的四指从a以不超过180度的转角转向b时，竖起的大拇指指向是c的方向）。但Unity是左手坐标系，所以这里应该是左手定则

1
2
// right是(1, 0, 0)    forward是(0, 0, 1)
Vector3.Cross(Vector3.right, Vector3.forward) = (0, -1, 0)

数乘运算

数乘是将向量的每个坐标值乘以该数值
$$
k \vec{v} = (k \times v_x, k \times v_y, k \times v_z)
$$

向量的概念

向量的模

返回向量的长度

1
float length = vector.magnitude;

向量的平方长度

返回向量的平方长度，通常用于比较向量大小而无需进行开方运算，从而提高效率

1
float sqrMagnitude = vector.sqrMagnitude;

单位向量

返回向量的单位向量，即长度为1但方向相同的向量

1
Vector3 normalizedVector = vector.normalized;

线性插值

在两个向量之间进行线性插值

1
Vector3 interpolatedVector = Vector3.Lerp(startVector, endVector, t);

两点之间的距离

返回两点之间的距离

1
float distance = Vector3.Distance(vectorA, vectorB);

向量之间的夹角

返回两个向量之间的夹角

1
float angle = Vector3.Angle(vectorA, vectorB);

投影向量

返回向量在另一个向量上的投影向量，一般是计算在坐标轴上的投影向量

1
Vector3 projectionVector = Vector3.Project(vectorToProject, ontoVector);

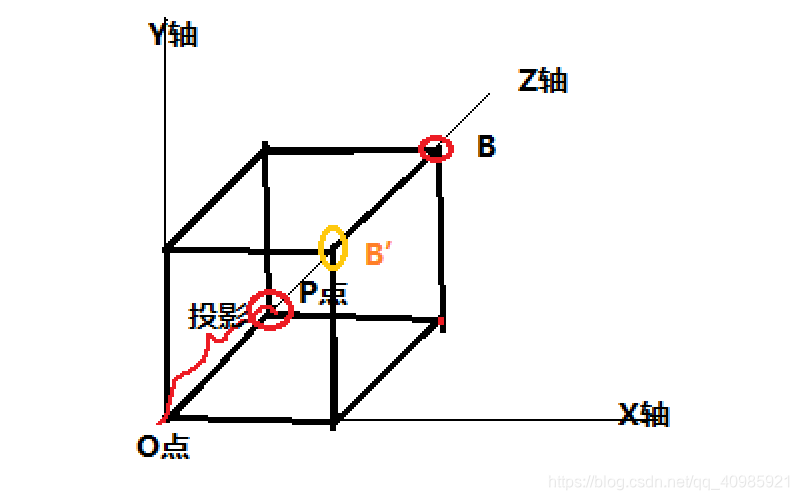
示例：

1
2
Vector3 B = new Vector3(2, 2, 2);
Vector3 result = Vector3.Project(B, Vector3.forward);    // 结果为 OP(0,0,2)

上图中是边长为2的正方形，OP是B在Z轴上的投影
B是B减去OP的向量，B(2,2,0) (向量本身减去此投影向量就为在平面上的向量)

反射向量

返回在另一个向量上的反射向量

1
Vector3 reflectionVector = Vector3.Reflect(incidentVector, normal);